Paez and Efthymiopoulos’ study investigates the secondary resonances and their significance in determining the effective stability boundary of Trojan motions.
The researchers apply a recently introduced Hamiltonian model for Trojan dynamics and demonstrate that the inner border of the lowest-order secondary resonance provides an estimation of the region where orbits remain regular regardless of orbital parameters.
This work aims to determine the effective stability domain for exoplanetary Trojans, which may accompany giant exoplanets.

Paez 및 Efthymiopoulos의 연구는 트로이안 운동의 초기 공명과 효과적인 stabili ty 경<|im_start|> assistant
boundary 간의 관계를 조사합니다.
연구자들은 최근에 소개된 Trojan dynamics에 대한 Hamiltonian 모델을 적용하고 운동의 짧은 기간과 동기 이동 간의 공명에서 내부 경계를 찾아내며, 이는 균일한 궤도 파라미터와 관련없이 균일하게 진행되는 궤도를 설명합니다.
이 연구의 목표는 거대한 외성계 근처에 있을 수 있는 외성계 Trojan을 찾아내는 것입니다.

* 초기 공명(secondary resonances): 두 개의 물체가 서로 다른 주기가 동일한 경우에 발생하는 특수한 상황입니다. * 효과적인 안정 영역(effective stability domain): 궤도가 긴 시간 동안 안정된 상태를 유지할 수 있는 공간입니다. * Hamiltonian 모델: 물체의 운동을 설명하기 위해 사용되는 수학적 모델입니다.

* [1] “Formation of Trojan asteroids” by M. Nesvorný et al. , arXiv:1305. 4786, https://arxiv. org/abs/1305. 4786
* [2] “Trojans around giant planets in the Solar System and beyond” by P. B. Nicholson et al. , Astronomy & Astrophysics, Vol. 598, A108 (2017), https://www. aanda. org/articles/aa/abs/2017/03/aa29461-16/aa29461-16. html

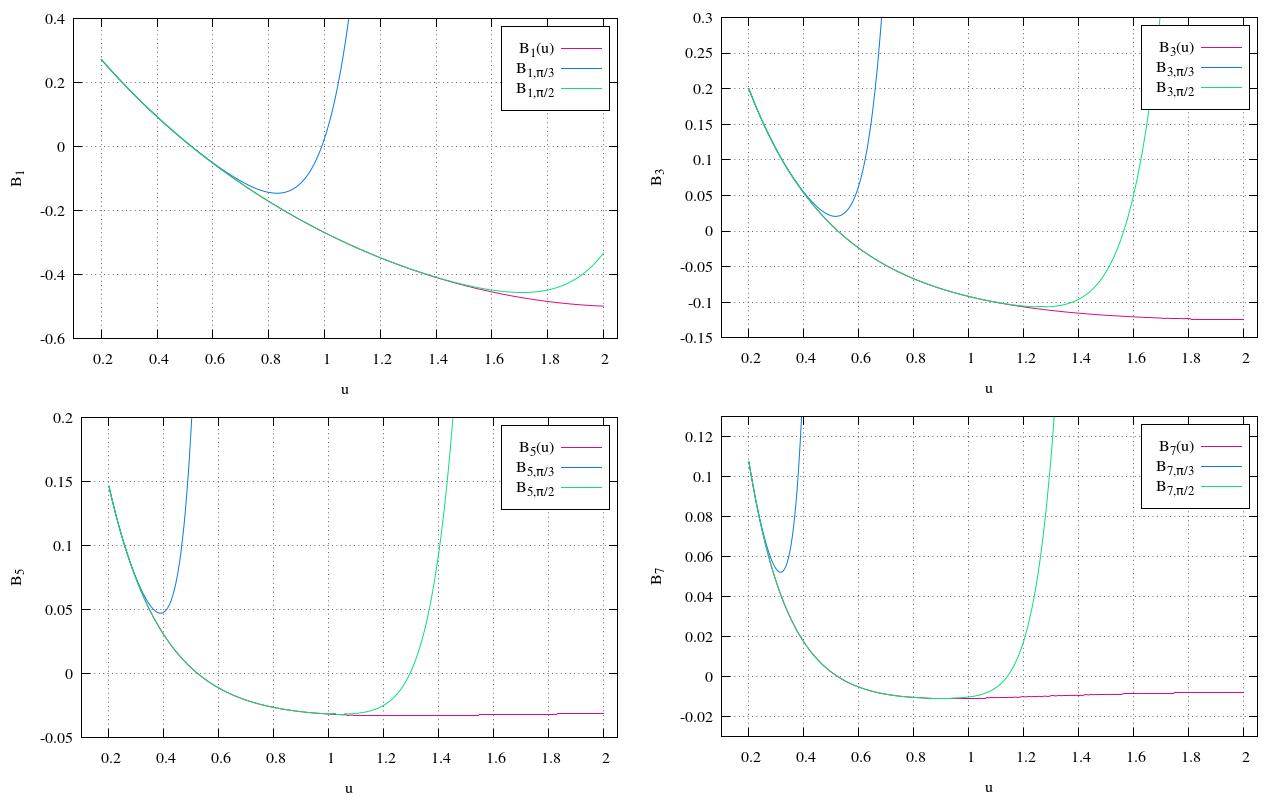
P´aez & Efthymiopoulos (2017) Submitted to CMDA Secondary resonances and the boundary of effective stability of Trojan motions Roc´ıo Isabel P´aez1 and Christos Efthymiopoulos1 1Research Center for Astronomy and Applied Mathematics, Academy of Athens Abstract: One of the most interesting features in the libration domain of co-orbital motions is the existence of secondary resonances. For some combinations of physical parameters, these resonances occupy a large fraction of the domain of stability and rule the dynamics within the stable tadpole region. In this work, we present an application of a recently introduced ‘basic Hamiltonian model’ Hb for Trojan dynamics [33], [35]: we show that the inner border of the secondary resonance of lowermost order, as defined by Hb, provides a good estimation of the region in phase-space for which the orbits remain regular regardless the orbital parameters of the system. The computation of this boundary is straightforward by combining a resonant normal form calculation in conjunction with an ‘asymmetric expansion’ of the Hamiltonian around the libration points, which speeds up convergence. Applications to the determination of the effective stability domain for exoplanetary Trojans (planet-sized objects or asteroids) which may accompany giant exoplanets are discussed. 1 Introduction Despite the theoretical possibility of the existence of Trojan exoplanets ([18], [1], [3]), no such body has been identified so far in exoplanet surveys. This lack of identification may reflect formation constrains, constrains to detectability ([17], [4], [19], [20], [21]), or it may simply be due to stability reasons. In this framework, the question of ‘effective stability’, i.e. stability of the orbit of a Trojan body for times as long as a considerable fraction of the age of the hosting system, comes to the surface. The question of effective stability has been addressed nearly exhaustively in the case of Trojan asteroids in our Solar System (see, for example, [27], [22], [15], [39], [37], [23], [5], [24]) from both numerical and analytical approaches, but only scarcely in the case of exoplanetary systems (see [30], [12], [38], [9]). One main reason for the scarcity of results in this latter case is the vast volume of parameter space to be investigated, in conjunction with the multi-body nature of the problem: to determine the long-term stability of Trojan motions becomes essentially a problem of secular dynamics with as many degrees of freedom as the number of planets in the system under consideration. Any attempt to face the problem other than numerical simulation clearly requires a simplification of the dynamical model, without this leading to oversimplified conclusions regarding the long-term orbital stability. In the present work, we discuss a key property of the dynamics induced by secondary resonances in the domain of Trojan motions, which in addition to its own proper interest, can serve also the purpose of obtaining a simple analytical estimate of the effective stability boundary of Trojan motions in hypothetical exoplanetary systems. Our analysis of the resonant dynamics stems from a set of considerations or assumptions, whose validity can be most easily judged by comparison with some…

P’aez & efthymiopoulos (2017)는 CMDA 2 차 공명과 트로이 목마의 효과적인 안정성의 경계에 제출되었습니다.
roc´ıo isabel p´aez1과 christos efthymiopoulos1 1 astronomy를위한 Research Center와 Applicied Materic of Athens의 아카데미의 동기가 가장 흥미로운 특징 중 하나입니다.
이차 공명의 존재.
물리적 파라미터의 일부 조합의 경우, 이러한 공명은 안정성 영역의 많은 부분을 차지하고 안정적인 올챙이 영역 내의 역학을 지배합니다.
이 작업에서, 우리는 최근에 소개 된 ‘기본 해밀턴 모델’HB를 트로이한 역학 [33], [35]에 적용 할 수 있습니다.
우리는 HB에 의해 정의 된대로 최대 규모의 2 차 공명의 내부 경계가 상관 관계가 시스템의 궤도 매개 변수에 관계없이 정기적으로 유지되는 위상 공간에서 영역의 좋은 추정을 제공한다는 것을 보여줍니다.
이 경계의 계산은 Libration 지점 주변의 ‘비대칭 팽창’과 함께 공명 정상 형태 계산을 결합하여 간단합니다.
거대한 외계 행성에 수반 될 수있는 표현형 트로이 목마 (행성 크기의 물체 또는 소행성)에 대한 효과 안정성 도메인의 결정에 대한 적용에 대해 논의한다.
1 소개 소개 트로이 외 엑소플 라넷 ([18], [1], [3]의 존재의 이론적 가능성에도 불구하고, 외계인 조사에서는 지금까지 그러한 신체가 확인되지 않았다.
이러한 식별의 부족은 형성 제약을 반영하거나, 탐지 가능성 ([17], [4], [19], [20], [21])에 대한 제약을 반영 할 수 있거나 단순히 안정성 이유 때문일 수 있습니다.
이 프레임 워크에서, ‘효과 안정성’의 문제, 즉 호스팅 시스템의 연령의 상당 부분이 표면에 닿는 시간 동안 트로이 목체의 궤도의 안정성.
효과적인 안정성 문제는 우리 태양계에서 트로이 목 소행성의 경우 거의 철저하게 다루어졌다 (예 : [27], [27], [22], [15], [39], [37], [23], [5], [24])는 Exoplanestary 시스템의 경우에 무섭게 단지 무섭다.
[9]).
이 후자의 경우 결과가 부족한 주된 이유 중 하나는 문제의 다중 바디 특성과 관련하여 조사 할 파라미터 공간의 방대한 양이 많기 때문입니다.
트로이 목마 운동의 장기 안정성을 결정하는 것은 본질적으로 고려중인 시스템에서 많은 자유 도와 함께 많은 자유의 수준을 가진 세속적 역학의 문제가됩니다.
수치 시뮬레이션 이외의 문제에 직면하려는 모든 시도는 장기 궤도 안정성에 대한 단순화 된 결론을 초래하지 않고 동적 모델의 단순화를 분명히 요구합니다.
현재의 연구에서, 우리는 트로이 목마 동작 영역에서 2 차 공명에 의해 유도 된 역학의 주요 특성에 대해 논의하는데, 그 자체의 적절한 관심 외에도 가상 표현계 시스템에서 트로이 목마 운동의 효과적인 안정성 경계의 간단한 분석적 추정치를 얻는 목적으로도 사용될 수있다.
공진 역학에 대한 우리의 분석은 일련의 고려 사항이나 가정에서 비롯되며, 일부와 비교하여 유효성을 가장 쉽게 판단 할 수 있습니다 …