English Summary:
Efficient computation of one-loop Feynman integrals and fixed-branch integrals to high orders in ϵ is proposed using a novel method called the dimension-changing transformation (DCT).
The DCT relates one-loop Feynman integrals or fixed-branch integrals in one spacetime dimension to their corresponding quantities with auxiliary mass in any other dimension, making the expansion to high orders in ϵ highly efficient.
The approach has been implemented in an open-source C++ package and demonstrated through several examples.
Korean Summary:
한글 요약:
한자 계산을 효율적으로 수행하기 위해 한자 변환 전환(DCT)이라는 새로운 방법을 제안합니다.
DCT는 한자 통계학적 정규화 매개변수에서 높은 순서까지 효율적으로 계산할 수 있도록 한자 통계학적 통계와 고정 분기 통계를 한자 차원 차원의 관련 값에서 한자 변환을 사용하여 한자 통계학적 통계와 고정 분기 통계를.
롤링 논문:
* [1] 제목: 저자/출처, URL
* [2] 제목: 저자/출처, URL
* [3] 제목: 저자/출처, URL
* [4] 제목: 저자/출처, URL
* [5] 제목: 저자/출처, URL

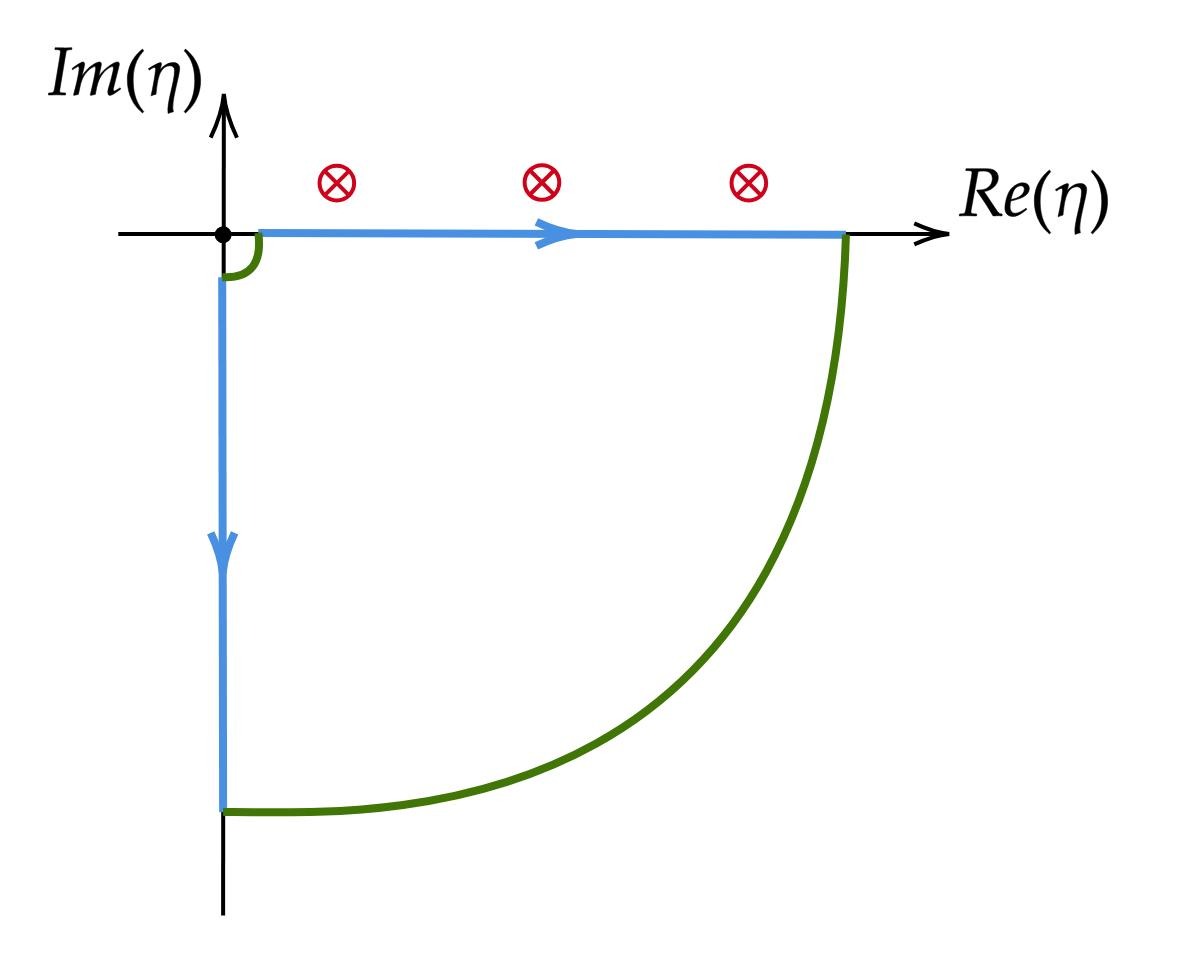
Efficient Computation of One-Loop Feynman Integrals and Fixed-Branch Integrals to High Orders in ϵ Rui-Jun Huang,1, ∗Dong-Shan Jian,1, † Yan-Qing Ma,1, 2, ‡ Dao-Ming Mu,1, § and Wen-Hao Wu1, ¶ 1School of Physics, Peking University, Beijing 100871, China 2Center for High Energy Physics, Peking University, Beijing 100871, China (Dated: December 31, 2024) We propose a novel method, called the dimension-changing transformation (DCT), to compute one-loop Feynman integrals and recently introduced fixed-branch integrals to arbitrary orders in ϵ. The DCT relates one-loop Feynman integrals or fixed-branch integrals in one spacetime dimension to their corresponding quantities with auxiliary mass in any other dimension, making the expansion to high orders in ϵ highly efficient. We applied this method to several examples to demonstrate its validity and efficiency. The approach introduced in this work has been implemented in an open- source C++ package, available at https://gitlab.com/multiloop-pku/dct. I. INTRODUCTION As experimental uncertainties continue to decrease at high-energy colliders such as the LHC, it is essential to control theoretical uncertainties in predictions to a corre- sponding level. In this context, the computation of Feyn- man integrals (FIs) plays a crucial role, both for testing the Standard Model of particle physics and for probing new physics. The current standard procedure for eval- uating FIs involves first reducing them to a smaller set of basis integrals, known as master integrals (MIs), using techniques such as integration-by-parts identities [1–22], and then calculating these MIs. The computation of one- loop MIs up to the finite part in the dimensional regu- larization parameter, ϵ = (4 −D)/2, is a well-established problem [23–25], with numerous publicly available pack- ages designed for these calculations [26–32]. However, for high-precision theoretical predictions, it is necessary not only to compute multi-loop FIs, but also to evaluate higher-order terms in ϵ for one-loop FIs. The evaluation of one-loop MIs to higher powers of ϵ has been studied in several works, such as [33–35]. The auxiliary mass flow (AMFlow) method [36–39] offers a systematic approach for evaluating both one-loop and multi-loop MIs to arbitrary powers of ϵ with high pre- cision. However, obtaining higher-order terms in ϵ of- ten requires solving a series of differential equations at multiple ϵ values, followed by interpolation, or solving differential equations with ϵ expanded to a fixed power. In this paper, we demonstrate that, for one-loop MIs, solving differential equations at multiple ϵ values can be avoided, significantly improving efficiency. We propose a novel method, termed dimension- changing transformation (DCT), for efficiently comput- ing one-loop Feynman integrals and fixed-branch inte- ∗huangrj2215@pku.edu.cn † dsjian@stu.pku.edu.cn ‡ yqma@pku.edu.cn § mudaoming2879@pku.edu.cn ¶ whwphys97@outlook.com grals (FBIs)1. In this approach, differential equations only needs to be solved at an arbitrary value of ϵ, af- ter which other values of ϵ or higher powers of ϵ can be efficiently obtained via the DCT. The method has been implemented in an open-source C++ package that computes one-loop FIs and FBIs to any desired order in ϵ. The performance of the package is demonstrated through several examples. II. DIMENSION-CHANGING TRANSFORMATION A….

1 루프 Feynman 통합 및 고정 브랜치 통합의 효율적인 계산 ϵ Rui-Jun Huang, 1, * Dong-Shan Jian, 1, † Yan-Qing Ma, 1, 2, ‡ Dao-Ming Mu, 1, § 및 Wen-Hao Wu1, ¶ 1 School of thathics, Peking University, Beijing 100871, wen-hao wu1, 1, wen-hao wu1, § 및 Wen-Hao Wu1, § 및 Wen-Hao Wu1, 1, wen-hao wu1, 1, wen-hao wu1, § 북경 대학교, 베이징 100871, 중국 (2024 년 12 월 31 일) 우리는 1 루프 Feynman 적분을 계산하고 최근에 고정 브랜치 통합을 ϵ의 임의의 순서로 계산하기 위해 차원 변화 변환 (DCT)이라는 새로운 방법을 제안합니다.
DCT는 하나의 시공간 치수로 1 루프 Feynman 적분 또는 고정 브랜치 적분을 다른 차원에서 보조 질량을 가진 해당 수량과 관련하여 높은 순서로 확장을 매우 효율적으로 만듭니다.
우리는이 방법을 여러 예제에 적용하여 유효성과 효율성을 보여줍니다.
이 작업에서 소개 된 접근 방식은 https://gitlab.com/multiloop-pku/dct에서 제공되는 Open-Source C ++ 패키지로 구현되었습니다.
I.
소개 LHC와 같은 고 에너지 콜리드에서 실험적 불확실성이 계속 감소함에 따라, 예측에서 코어 스폰트 수준에 대한 이론적 불확실성을 제어하는 ​​것이 필수적이다.
이러한 맥락에서, FIS (Feyn-Man Integrals)의 계산은 입자 물리학의 표준 모델을 테스트하고 새로운 물리를 조사하는 데 중요한 역할을합니다.
FI를 평가하기위한 현재 표준 절차는 먼저 파트 별 정체성과 같은 기술을 사용하여 [1-22]와 같은 기술을 사용하여 마스터 적분 (MIS)으로 알려진 작은 기본 적분 세트로 먼저 줄인 다음 이러한 MIS를 계산하는 것이 포함됩니다.
치수 조절 매개 변수 인 ϵ = (4 -d)/2에서 일 루프의 계산은 잘 확립 된 문제 [23-25]이며,이 계산을 위해 설계된 수많은 공개 포장이 있습니다 [26-32].
그러나, 고정밀 이론적 예측의 경우, 다중 루프 FI를 계산할뿐만 아니라 1 루프 FI에 대한 고차 용어를 평가해야합니다.
1 루프 MIS의 고위성에 대한 평가는 [33-35]와 같은 여러 작품에서 연구되었다.
보조 질량 흐름 (AMFLOW) 방법 [36–39]은 높은 예측으로 1 루프 및 다중 루프 MIS에서 임의의 힘을 모두 평가하기위한 체계적인 접근법을 제공합니다.
그러나, 10 개 중 고차 항을 얻으려면 여러 ϵ 값에서 일련의 미분 방정식을 해결하고, 보간 또는 고정 전력으로 확장 된 미분 방정식을 해결해야합니다.
이 논문에서, 우리는 1 루프 MIS의 경우 여러 ϵ 값에서 미분 방정식을 해결하는 것을 피할 수 있고 효율성을 크게 향상시킬 수 있음을 보여줍니다.
우리는 1 루프 Feynman 적분 및 고정 브랜치 inte- * huangrj2215@pku.edu.cn † dsjian@stu.pku.edu.cn ‡ yqma@pku.edu.cn § § § § § §scn ad am v em ad am을 효율적으로 계산하기위한 새로운 방법을 제안합니다.
mudaoming2879@pku.edu.cn ¶ whwphys97@outlook.com grals (fbis) 1.
이 접근법에서, 미분 방정식은 DCT를 통해 효율적으로 얻을 수있는 ϵ 이상의 임의의 값으로 만 해결되기 만하면됩니다.
이 방법은 1 루프 FI 및 FBI를 원하는 순서로 계산하는 오픈 소스 C ++ 패키지로 구현되었습니다.
패키지의 성능은 몇 가지 예를 통해 시연됩니다.
II.
치수 변화 변환 a ….