Summary (English)
This scientific paper explores the dynamics of nonlinear electromagnetism, specifically the “ModMax” theory.
ModMax is a recently proposed extension of Maxwell’s theory that preserves its symmetries and has applications in studying regular black hole solutions and supersymmetry.
The main objectives of this study include understanding the initial-value problem for ModMax, proving geometric inequalities relating energy, charge, angular momentum, and size, and performing stable numerical simulations in highly nonlinear regimes to verify these inequalities.
The results show that ModMax admits a well-posed formulation, supports Bekenstein’s universal inequality conjecture for macroscopic systems, and provides insights into its consistency as a theory.
ModMax is a recently proposed extension of Maxwell’s theory that preserves its symmetries and has applications in studying regular black hole solutions and supersymmetry.
The main objectives of this study include understanding the initial-value problem for ModMax, proving geometric inequalities relating energy, charge, angular momentum, and size, and performing stable numerical simulations in highly nonlinear regimes to verify these inequalities.
The results show that ModMax admits a well-posed formulation, supports Bekenstein’s universal inequality conjecture for macroscopic systems, and provides insights into its consistency as a theory.
요약 (Korean)
이 과학 논문은 비선형 전자기, 특히 “Modmax”이론의 역학을 탐구합니다.
Modmax는 최근에 제안 된 Maxwell의 이론 확장으로 대칭을 보존하고 일반 블랙홀 솔루션 및 초대칭을 연구하는 데 응용 프로그램이 있습니다.
이 연구의 주요 목표는 Modmax의 초기 가치 문제를 이해하고, 에너지, 전하, 각 운동량 및 크기와 관련된 기하학적 불평등을 입증하며, 이러한 불평등을 확인하기 위해 고도로 비선형 체제에서 안정적인 수치 시뮬레이션을 수행하는 것입니다.
결과는 Modmax가 잘 알려진 공식을 인정하고 거시적 시스템에 대한 Bekenstein의 보편적 불평등 추측을 지원하며 이론으로서의 일관성에 대한 통찰력을 제공한다는 것을 보여줍니다.
Modmax는 최근에 제안 된 Maxwell의 이론 확장으로 대칭을 보존하고 일반 블랙홀 솔루션 및 초대칭을 연구하는 데 응용 프로그램이 있습니다.
이 연구의 주요 목표는 Modmax의 초기 가치 문제를 이해하고, 에너지, 전하, 각 운동량 및 크기와 관련된 기하학적 불평등을 입증하며, 이러한 불평등을 확인하기 위해 고도로 비선형 체제에서 안정적인 수치 시뮬레이션을 수행하는 것입니다.
결과는 Modmax가 잘 알려진 공식을 인정하고 거시적 시스템에 대한 Bekenstein의 보편적 불평등 추측을 지원하며 이론으로서의 일관성에 대한 통찰력을 제공한다는 것을 보여줍니다.
기술적 용어 설명 (Technical Terms)
추출된 기술 용어가 없습니다.
Excerpt (English Original)
Bekenstein bounds in maximally symmetric nonlinear electrodynamics Juan M.
Diaz1∗and Marcelo E.
Rubio2,3,4† 1Aix Marseille University, 3 Pl.
Victor Hugo, 13003 Marseille, France 2Gran Sasso Science Institute (GSSI), Viale Francesco Crispi 7, I-67100 L’Aquila, Italy 3INFN, Laboratori Nazionali del Gran Sasso, I-67100 Assergi, Italy 4SISSA, Via Bonomea 265, 34136 Trieste, Italy We explore dynamical features of the maximally symmetric nonlinear extension of classical elec- tromagnetism, recently proposed in the literature as “ModMax” electrodynamics.
This family of theories is the only one that preserves all the symmetries of Maxwell’s theory, having applications in the study of regular black hole solutions and supersymmetry.
The purpose of this article is three-fold.
Firstly, we study the initial-value problem of ModMax and show, by means of a simple geometric criterion, that such a theory admits a well-posed formulation.
Secondly, we prove a series of geometric inequalities relating energy, charge, angular momentum, and size in ModMax.
The validity of these bounds gives strong evidence of an universal inequality conjectured by Bekenstein for macroscopic systems.
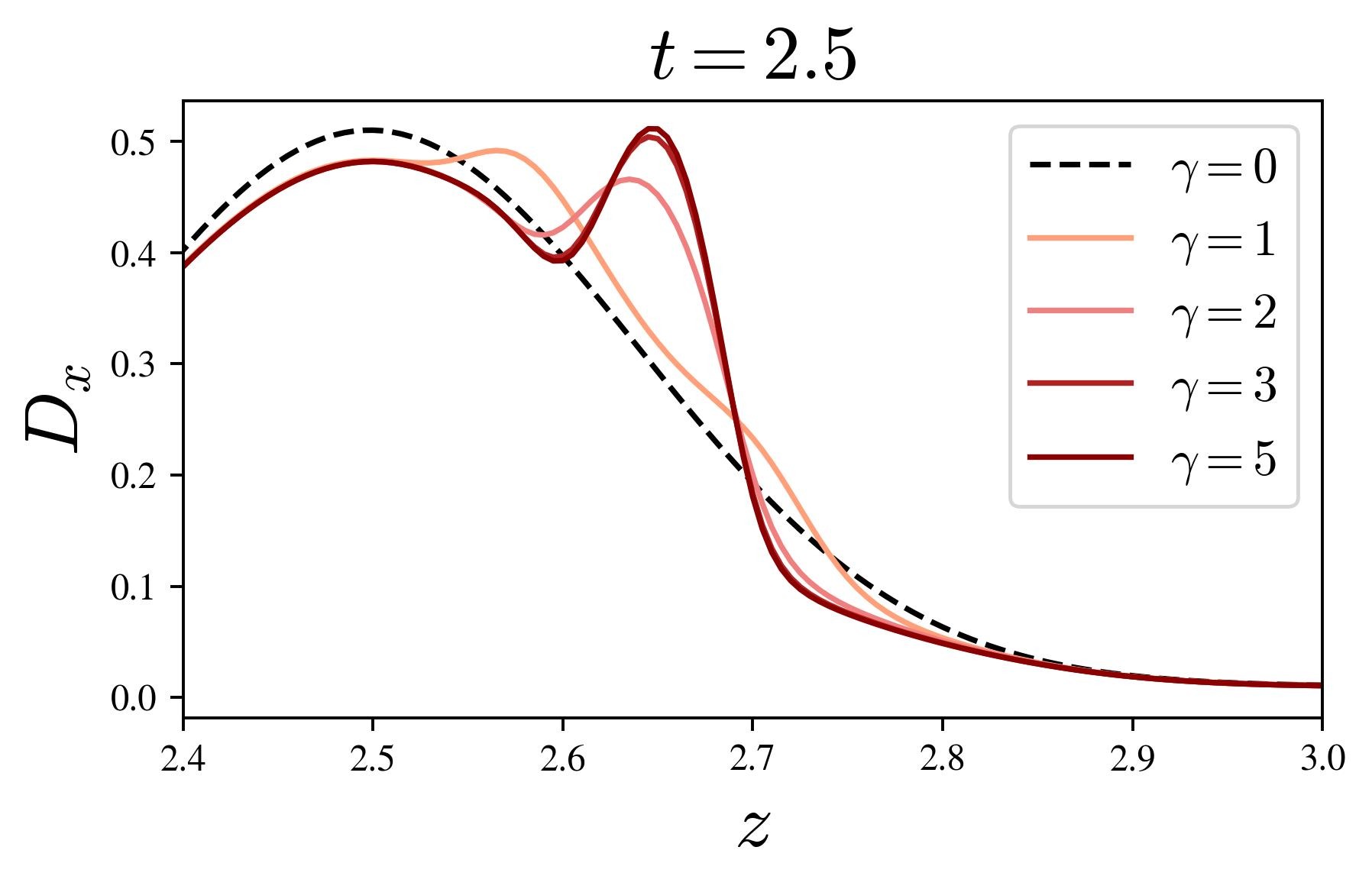
Finally, we perform the first stable numerical simulations of ModMax in the highly nonlinear regime, and verify an inequality between energy, size and angular momentum2024 in bounded domains.
I.
INTRODUCTION quantum theory or effective modified gravitational theoryDec that explains the dynamics of the spacetime surrounding The first proposal of a nonlinear theory for electro- the singularity.
Remarkably, by coupling NLED to grav-23 magnetism came up in the early 30’s, developed by Born ity, it is possible to construct stable and regular black- and Infeld with the aim to resolve the singularity of the hole solutions, thus avoiding the development of physical electric field produced by a point charge [1].
Since then, singularities [18–21].
nonlinear extensions of classical electrodynamics have at- From a general perspective, nonlinear extensions of tracted attention, akin their applications…
Diaz1∗and Marcelo E.
Rubio2,3,4† 1Aix Marseille University, 3 Pl.
Victor Hugo, 13003 Marseille, France 2Gran Sasso Science Institute (GSSI), Viale Francesco Crispi 7, I-67100 L’Aquila, Italy 3INFN, Laboratori Nazionali del Gran Sasso, I-67100 Assergi, Italy 4SISSA, Via Bonomea 265, 34136 Trieste, Italy We explore dynamical features of the maximally symmetric nonlinear extension of classical elec- tromagnetism, recently proposed in the literature as “ModMax” electrodynamics.
This family of theories is the only one that preserves all the symmetries of Maxwell’s theory, having applications in the study of regular black hole solutions and supersymmetry.
The purpose of this article is three-fold.
Firstly, we study the initial-value problem of ModMax and show, by means of a simple geometric criterion, that such a theory admits a well-posed formulation.
Secondly, we prove a series of geometric inequalities relating energy, charge, angular momentum, and size in ModMax.
The validity of these bounds gives strong evidence of an universal inequality conjectured by Bekenstein for macroscopic systems.
Finally, we perform the first stable numerical simulations of ModMax in the highly nonlinear regime, and verify an inequality between energy, size and angular momentum2024 in bounded domains.
I.
INTRODUCTION quantum theory or effective modified gravitational theoryDec that explains the dynamics of the spacetime surrounding The first proposal of a nonlinear theory for electro- the singularity.
Remarkably, by coupling NLED to grav-23 magnetism came up in the early 30’s, developed by Born ity, it is possible to construct stable and regular black- and Infeld with the aim to resolve the singularity of the hole solutions, thus avoiding the development of physical electric field produced by a point charge [1].
Since then, singularities [18–21].
nonlinear extensions of classical electrodynamics have at- From a general perspective, nonlinear extensions of tracted attention, akin their applications…
발췌문 (Korean Translation)
Bekenstein은 최대 대칭 비선형 전기 역학에서 경계 Juan M.
diaz1 * 및 Marcelo E.
Rubio2,3,4 † 1aix Marseille University, 3 pl.
Victor Hugo, 13003 Marseille, France 2gran Sasso Science Institute (GSSI), Viale Francesco Crispi 7, I-67100 L ‘Aquila, Italy 3infn, Nazionali del Gran Sasso, I-67100 Assergi, Italy 4Sissa, BoNOMEA 265, 34136 TREASE, INOVERSE, INOVERSE 최근 문헌에서“modmax”전기 역학으로 제안 된 고전적인 전자기의 최대 대칭 비선형 확장.
이 이론의 가족은 Maxwell 이론의 모든 대칭을 보존하는 유일한 이론입니다.
일반 블랙홀 솔루션 및 초대칭 연구에 적용됩니다.
이 기사의 목적은 세 가지입니다.
첫째, 우리는 단순한 기하학적 기준을 통해 이러한 이론이 잘 정식 된 공식을 인정한다는 간단한 기하학적 기준을 통해 Modmax의 초기 가치 문제를 연구합니다.
둘째, 우리는 Modmax에서 에너지, 전하, 각 운동량 및 크기와 관련된 일련의 기하학적 불평등을 증명합니다.
이 경계의 타당성은 거시적 시스템에 대해 Bekenstein이 추측 한 보편적 불평등의 강력한 증거를 제공합니다.
마지막으로, 우리는 비선형 체제에서 Modmax의 첫 번째 안정적인 수치 시뮬레이션을 수행하고, 경계 도메인에서 에너지, 크기 및 각도 Momentum2024 사이의 불평등을 확인합니다.
I.
소개 양자 이론 또는 효과적인 변형 중력 이론은 전기성에 대한 비선형 이론의 첫 번째 제안을 둘러싼 시공간의 역학을 설명하는 효과적인 수정 된 중력 이론.
놀랍게도, Born Ity가 개발 한 30 년대 초반에 Nled Nled Nled to Grav-23 자성이 등장함으로써, 홀 용액의 특이성을 해결하기 위해 안정적이고 규칙적인 블랙을 구성 할 수 있으며, 따라서 포인트 전하에 의해 생성 된 물리적 전기장의 발달을 피할 수 있습니다 [1].
그 이후로 특이점 [18–21].
고전적인 전기 역학의 비선형 확장은 일반적인 관점에서, 트랙트주의의 비선형 연장, 적용을 유사하게 …
diaz1 * 및 Marcelo E.
Rubio2,3,4 † 1aix Marseille University, 3 pl.
Victor Hugo, 13003 Marseille, France 2gran Sasso Science Institute (GSSI), Viale Francesco Crispi 7, I-67100 L ‘Aquila, Italy 3infn, Nazionali del Gran Sasso, I-67100 Assergi, Italy 4Sissa, BoNOMEA 265, 34136 TREASE, INOVERSE, INOVERSE 최근 문헌에서“modmax”전기 역학으로 제안 된 고전적인 전자기의 최대 대칭 비선형 확장.
이 이론의 가족은 Maxwell 이론의 모든 대칭을 보존하는 유일한 이론입니다.
일반 블랙홀 솔루션 및 초대칭 연구에 적용됩니다.
이 기사의 목적은 세 가지입니다.
첫째, 우리는 단순한 기하학적 기준을 통해 이러한 이론이 잘 정식 된 공식을 인정한다는 간단한 기하학적 기준을 통해 Modmax의 초기 가치 문제를 연구합니다.
둘째, 우리는 Modmax에서 에너지, 전하, 각 운동량 및 크기와 관련된 일련의 기하학적 불평등을 증명합니다.
이 경계의 타당성은 거시적 시스템에 대해 Bekenstein이 추측 한 보편적 불평등의 강력한 증거를 제공합니다.
마지막으로, 우리는 비선형 체제에서 Modmax의 첫 번째 안정적인 수치 시뮬레이션을 수행하고, 경계 도메인에서 에너지, 크기 및 각도 Momentum2024 사이의 불평등을 확인합니다.
I.
소개 양자 이론 또는 효과적인 변형 중력 이론은 전기성에 대한 비선형 이론의 첫 번째 제안을 둘러싼 시공간의 역학을 설명하는 효과적인 수정 된 중력 이론.
놀랍게도, Born Ity가 개발 한 30 년대 초반에 Nled Nled Nled to Grav-23 자성이 등장함으로써, 홀 용액의 특이성을 해결하기 위해 안정적이고 규칙적인 블랙을 구성 할 수 있으며, 따라서 포인트 전하에 의해 생성 된 물리적 전기장의 발달을 피할 수 있습니다 [1].
그 이후로 특이점 [18–21].
고전적인 전기 역학의 비선형 확장은 일반적인 관점에서, 트랙트주의의 비선형 연장, 적용을 유사하게 …
출처: arXiv
답글 남기기